Game Programming


Games are the rocket science of computer programming. If you can program a good game, you can do anything. This is because the technologies used in making a satisfactory game cover all the hardest parts of computer programming: artificial intelligence, graphics and animation, human interface, database management, net communications, physics and math, real-time control, state machines, team development, all of these are important in modern computer game play. Some of the better recent games also exhibit learning and natural-language processing. You can get a whole college degree majoring just on programming games, and this tutorial is not even a single college course. We will touch on just a few of the essentials here, with a couple of very simple games.
 

Tic-Tac-Toe

The strategy and the game board presentation for Tic-Tac-Toe are both relatively simple, and most people learn the game at an early age. This makes it an easy programming example. Not counting rotations and reflections, there are fewer than a half-dozen optimal strategies for playing the game, which is well within the ability of a programmer who has successfully completed the tutorial this far to program. That would be boring.

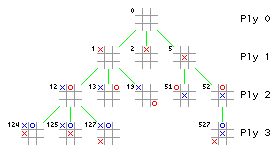
Instead, we will introduce you to a simple artificial intelligence (AI) technique for doing turn-based strategy games like checkers and chess, where the number of different possible games is astronomical and intractable for exhaustive programming. The technique is called "depth-first search" which is further refined to "alpha-beta pruning" from the fact that it "prunes" the game tree to the interesting and most probable future game plays. A computer "tree" is a set of imaginary nodes -- typically data points -- connected in such a way that there is only connection path between any two of them. In a game tree, the nodes are the state of the play after each possible turn. The first node in our Tic-Tac-Toe game is of course the empty board. X (who always plays first) can play one of three distinct squares (not counting reflections and rotations), giving three new nodes, each connected by a line to the first, thus:

The root node (numbered 0 in this diagram) is at the top, because computer trees are usually shown growing down instead of up. The branches (called arcs) are shown in green, and show the different ways the game can progress. All the possible game boards after two turns of play is called ply 2, perhaps after plywood layers. I have chosen to number the nodes by the positions played so far (in order), where the top left position is 1, top center is 2, and so on. You can number the board squares any way that makes sense. This one has the convenience that it shows the complete game history, and we can also infer the board display from the number.

I did not show them all, but you should convince yourself that O has five unique possible plays under node 1, and five more plays under node 2, but only two distinct plays (both shown) under node 5. The tree has been pruned at this level, that is, some of the branches were cut off (not examined). To look at all of them gets very detailed and expensive of computer time. For games like chess, it becomes impossible.

X has a very good play under node 52, which forces a win, and at least three win-forcing plays under node 12. If X plays reasonably well, O never gets any win-forcing plays. However, O can, with prudent play, force a tie. Alpha-beta pruning is a game strategy that does not waste computer time on unlikely or losing game nodes, that is, it prunes them from the game tree. The first player is historically called by the first Greek letter, Alpha, and the second by the second Greek letter, Beta.

When the computer is analyzing where to play on its next turn, it has no way of knowing if any particular square is a good or bad play -- unless that play completes the winning 3-in-a-row. Obviously, if it results in a win, the computer should play that square. Otherwise, it tries each available square in turn, then turns around and tries to play its opponent by the same rules. If the opponent has a winning move, we assume it will be taken, so the preceding computer move is a very bad (losing) move, and scored very low. If there are no wins at that ply, the computer then tries all possible plays at the next ply. Each winning play reflects back on the previous ply as a low (or negative number) for that play, and each losing play reflects back on the previous ply as a good (high-score) number. When there are several choices, the scores might be averaged, or else the worst scores simply discarded (pruned) because no sensible player would play such a losing game.

In the game above, alpha-beta pruning would show that play 51 results in a worst-case tie, while 52 results in a lose. Therefore 52 is pruned away, and Beta (O) plays 51. Alpha, deciding where to make its first play, recognizes that Beta would choose 51 over 52, so it scores play 5 as a draw. Walking down each ply, one at a time, is called depth-first search, because it is wasteful of computer memory to build a whole ply at each level. Instead we try one position, then analyze the next level before trying the next position at this level. This way we only need to retain in memory all the intermediate games in a particular path from the root node to the board currently being analyzed (recall all of that information is retained in the node number). Then we back-track to the next level up and go down the next branch of the tree at that level, and so on.

Now that we have the strategy worked out, it only remains to program it and the turns-taking interaction. Ordinarily (in most programming languages) the game program would remain in control for the whole game, but JavaScript has very lame input and output capabilities, so we will delve into HTML for some of the interaction and display.

First the display. HTML has a table structure that will serve to display the rows and columns lined up correctly. Our table looks like this in HTML:

<table BORDER COLS=3 WIDTH=62 >
<tr>
<td ALIGN=CENTER>1</td>
<td ALIGN=CENTER>2</td>
<td ALIGN=CENTER>3</td>
</tr>
<tr>
<td ALIGN=CENTER>4</td>
<td ALIGN=CENTER>5</td>
<td ALIGN=CENTER>6</td>
</tr>
<tr>
<td ALIGN=CENTER>7</td>
<td ALIGN=CENTER>8</td>
<td ALIGN=CENTER>9</td>
</tr>
</table>
The header allows about 20 pixels width for each of three columns, with 2 extra pixels for the table edge. We will generate this text using document.write() commands, which you already know about. I observed that my browser does not display the cell boundaries unless there is  actual text there to display, so I leave the numbers there. What we really want is for the user to be able to click on a number to play that square. An HTML link that calls a JavaScript function looks like this:
<a href="Javascript:functionName(arguments)">display text</a>
Notice the quotation marks. These can be generated by including a back-slash escape before each quote in the string literal. The generated text for our (empty) Tic-Tac-Toe board ready for the user to play X should look like this:
<table BORDER COLS=3 WIDTH=62 >
<tr>
<td ALIGN=CENTER><a href="Javascript:play(1)">1</a></td>
<td ALIGN=CENTER><a href="Javascript:play(2)">2</a></td>
<td ALIGN=CENTER><a href="Javascript:play(3)">3</a></td>
</tr>
<tr>
<td ALIGN=CENTER><a href="Javascript:play(4)">4</a></td>
<td ALIGN=CENTER><a href="Javascript:play(5)">5</a></td>
<td ALIGN=CENTER><a href="Javascript:play(6)">6</a></td>
</tr>
<tr>
<td ALIGN=CENTER><a href="Javascript:play(7)">7</a></td>
<td ALIGN=CENTER><a href="Javascript:play(8)">8</a></td>
<td ALIGN=CENTER><a href="Javascript:play(9)">9</a></td>
</tr>
</table>
We can easily generate this in a function with 2 nested for-loops (or else a single for-loop with a row-end test). Try it yourself both ways now, before looking at my hints.

We are not done yet. We really want this display function to be smarter, so it shows the unplayed squares as links, and the played squares respectively as Xes and Os. Recalling our node-numbering convention above, we can pass the node number as a parameter, then display either X or O if that square number is in the parameter. How do you know whether it is X or O? X always plays first, so the indexOf for that digit will be even if it's X, and odd if O. Modify your function(s) to accept a node number parameter. When I tried it, I got no table at all, because the indexOf() method only works for string variables, and I was giving it a number. I had not realized that limitation, but my Jscript interpreter found the problem for me. I solved it by putting quotes around the node number ("52739") I was using to test it. Try to make your function work before looking at how I did it.

The user input is rather trickier than it should have been. When the (human) player clicks on a square number link, it will call function play() with that number as a parameter. So far this has been just a stub in my examples. Now, what we want it to do is take the previous game node, concatenate this square number on the end, and redisplay the board with this new node number. I created a variable

var sofar = "";
and then inside the ShoGame(node) function, set
sofar = node;
Function play(whom) becomes very simple:
function play(whom) {ShoGame(sofar+""+whom);}
The extra empty string concatenation forces the "+" to be string concatenation instead of number addition. As I said earlier, it was a foolish decision on the part of the language designer, but we must now live with their folly. Life is like that.

This works in my browser for one play only, because the next time I click on a number, it can't find the play() function. It seems that redrawing the window erased the script. Clicking on the browser Reload button (in my browser) restored the script, but lost the game state. I solved this with some more HTML and a couple more built-in JavaScript properties, "location.href" and "location.hash" which return the full URL of the current page, and just the "hash" part of it (these are known to the current Jscript interpreter, but obviously cannot behave properly).

Still working in my browser (Netscape 4.73), when I assign a value to the location.href property, that page is fetched and drawn (unless it's the same page already displaying, which is a second problem, that we'll get to later). We can use the hash portion to carry the current game state. So if your Tic-Tac-Toe page is in the file "C:\JavaScript\TicTacToe.html" then to display the game state 52739 we would ask the browser to display "C:\JavaScript\TicTacToe.html#52739" then modify our script thus:

var pageLoc = location.href;
var sofar = location.hash;
if (sofar != "") {
  pageLoc = pageLoc.substr(0,pageLoc.length-sofar.length);
  sofar = sofar.substr(1);}

function play(whom) {location.href = pageLoc+"#"+sofar+whom;}

ShoGame(sofar);

When I did this, the URL on the location bar changed, but the page did not refresh. However, the Reload button did update it with the current game state. There is a location.reload(false) method that effectively pushes the Reload button from your program. Unfortunately, this went into an infinite loop for me, continually refreshing the window. I needed to be very careful to call this method only when changing the game state. Since the game state is preserved only in the hash, we need a special marker that says this is a new update. I put an underscore at the end of the hash in the play() function, then removed it when the page loaded:
var pageLoc = location.href;
var sofar = location.hash;
var nuly = sofar.indexOf("_");
if (sofar != "") {
  pageLoc = pageLoc.substr(0,pageLoc.length-sofar.length);
  if (nuly>0) {
    sofar = sofar.substr(0,nuly);
    location.href = pageLoc+sofar;}
  sofar = sofar.substr(1);}

function play(whom) {location.href = pageLoc+"#"+sofar+whom+"_";}

ShoGame(sofar);

This didn't work as expected, but with some fiddling around I was able to get it to reload properly by setting the location at the end of the ShoGame() function, but only if I also passed in as a parameter the page URL (because it was gone after the board got redrawn). One thing you will learn in programming: what they tell you about the language you are programming in is not perfectly reliable, and you may need to (as one reference manual candidly advised) "randomly re-arrange program elements" until it works. Maybe not randomly, but try different ideas. You need to think like a computer; the people who write the reference material don't always do it for you. It turned out I did not need the location.reload(false) method at all, because the redraw effectively changed the page title, which made changing the location property functional again.

Anyway, I got it working on my computer (classic Mac), but then I tried it on a PC, and WindowsExplorer errored off when the display was redrawn. So I added code to wrap page header and body tags around the table when a new play refreshed it. That fixed the error, but WindowsExplorer absolutely refused to reload the file with the changed location, so the JavaScript code was not available for subsequent play. Microsoft is famous for subverting standards and doing things just plain wrong. Everybody must make allowances for the 800 pound gorilla in the room. I solved the problem by making two identical files that differ only slightly in their names, then tweaking the name to refer to the other file when I loaded the location. It now works in both browsers available to me, but if you are using yet some other browser, who knows?

You probably need to look at my code to see everything I did. If you click on this link, it will open the current version of the game in your browser. View the page source (in your browser) or else open "TicTacZed.html" and "TacTicZed.html" in your text editor to see the program code. Notice that I added a "New Game" link and function to clear the board and restart. At this point, the game is suitable for two people to play each other, except the computer does not notice when one of them wins. Let's add that in next...

I couldn't think of any elegant way to determine if one side or the other has won, other than by trying all possible combinations. We don't know the order of the plays in the current game state, only that the even-position digits are Xes and the odd ones are Os. We also know (from the way it is constructed) that there are no duplicates. If you don't mind some binary numbers, we can add up the bits representing all the Xes in the game state, then compare it to each number in a list of winners (there are three rows, three columns, and two diagonals). Position 1 adds 21 to the position value; 2 adds 22 (=4); 3 adds 23 (=8), and so on. This is easy in C-based languages, you just use the bit-shift operator, thus:

ofx = 0;
for (ix=0; ix<node.length; ix+=2)
  ofx = ofx+(1<<(node.substr(ix,1)-0));
Here, node.substr(ix,1) extracts a single digit at position ix, then subtracting zero converts the (text) digit to a number, which is used to shift 1 left that many places, effective 2 raised to that power. We know what the bits for winning rows are: 21+22+23=14, 24+25+26=112, and 27+28+29=896. I leave as an exercise calculating the winning columns and diagonals. The total X positions played might extend onto other rows or columns, so we also must trim the number being tested to the current row or column. I test each one in turn, and set the sum to zero if it's none of them:
if ((ofx&14) != 14) if ((ofx&112) != 112) if ((ofx&896) != 896) // three rows
  if ((ofx&146) != 146) if ((ofx&292) != 292) if ((ofx&584) != 584) // 3 cols
    if ((ofx&546) != 546) if ((ofx&168) != 168) ofx = 0; // two diagonals
if (ofx>0) document.write("<p><b>X</b> won!!<p>");
If X didn't win, maybe O did. You can see where this goes:
else { // X did not win, try O..
  for (ix=1; ix<node.length; ix+=2)
You could put this either before or after drawing the game board. Of course nothing stops the players from continuing to play after somebody won. How would you prevent that?
 

Computer Play

Now we are ready for the hard part. Somebody needs to decide whether the computer plays first, or the human, but we can leave that for later. Let's write a function to choose a position to play, based on depth-first search. It will be recursive: given a current game state, it will try each unoccupied square in turn, assume it played that position, see if it won, and if so, return that play as best. Otherwise it sends this new game state to itself to pick a best move for the opponent, scoring each position by how close it is to winning (or losing, negative). The highest scored position is returned. Notice that we flip the signs at each recursion, so what is best for Beta is worst for Alpha, and vice versa.

First I moved the win test into a separate function Xwon(Gstate). It's only necessary to test if X won, because the same function can be called again with the first digit removed from the game state to know if O won. This test had to be at the beginning of the board display routine, because all the JavaScript (except currently active functions) disappears in the browser as soon as we start to display anything. Making it a separate function means I can also call it from my move evaluator. The move evaluator is called before any display takes place, so all the functions are still there and visible.

The move evaluator, which I called BestMove(Gstate), needs to return two pieces of information, the best square, and how good it is. A function normally only returns one value, but I can pack these two numbers into one by multiplying the score by some power of two greater than the highest square position (9), then adding the chosen position. I can subsequently extract the position using the & operator; the score can be used as is, since all I do is compare it to other scores. We could use an array to keep the scores, where all the occupied positions are scored very negative so they cannot be played, but I decided to test for the best score on the fly. A single number packs the played bits, the same as we did for win-testing:

function BestMove(Gstate) {
  var best = -99<<10; // worst possible score, if nothing can be played
  var board = 0;
  var lxx = Gstate.length;
  var ix = 0;
  var nx = 0;
  var try = "";
  if (lxx==9) return 0; // cats game
  for (ix=0; ix<lxx; ix++) // collect played positions..
    board = board+(1<<(Gstate.substr(ix,1)-0));}
  for (ix=1; ix<=9; ix--) {
    if ((board&(1<<ix)) !=0) continue; // already taken
    try = Gstate+""+ix;
    if ((lxx&1)==0) { // playing X..
      if (Xwon(try)) return (99<<10)+ix;} // best possible score
    else if (Xwon(try.substr(1))) return (99<<10)+ix;} // ditto as O
    nx = -BestMove(try)>>1;
    if (best<nx) best = (nx&-16)+ix;} // save best
  return best;}
The last two lines of the second loop require some explanation. The recursive result might determine that the next move is a win, which is a very large number. We cut the negative of that number in half (shift right by 1 position). Since a win score is 99 shifted left ten places, and there are at most nine plays, the resulting score will always be 198 or larger (or else negative), unless the game is a draw, which returns zero or the play that gets to a draw.

Binary 15 is 1111, which would mask or trim off all but the play number saved in best in the last line of the loop. Binary -16 is the opposite mask, zero in the low four bits, and ones all the way up from there. The & operator forces to zero all the bits of the other operand where the mask is zero, which in this case leaves a hole in the number to keep the play in.

Let's watch this in action. When BestMove("") is called with an empty board, the first play tested is square 1, which is passed as a parameter to the recursive call of BestMove("1"). It can't play 1, so it tries 2, and sends "12" to the recursive call, and so on, which fills up the board as a checkerboard when it reaches the 9th call. This is a draw, which is better than the default, so best is set to half of the returned zero plus the played 9, =9. This is again better than the default, so best is set to a half of the negative of the returned 9, which is -4, masked by -16, plus the played 8, which is -8. Here is binary 9:

  0000000000001001
Here is -9:
  1111111111110111
Shift right one place (negative numbers stay negative through shifts):
  1111111111111011
ANDed to -16:
  1111111111111011
& 1111111111110000
= 1111111111110000
Add 8:
  1111111111110000
+ 0000000000001000
= 1111111111111000
The next return again takes the negative half of this, which is +4, but that is masked out and replaced by the play 7, and so on back to the beginning. Some of the recursive calls will be wins for X, which will be immediately pruned back in the previous O analysis, unless it is a forced win, which it sends back as a large negative number. At that ply the number is converted to a (not-so-large) positive number, which is still very good, but it's again negative in the previous ply, where one of the draw plays looks better.

If every play is tested at every level, you have 9! (factorial 9, = 362,880) individual tests for the first play. I manually pruned the game tree at the first two levels to remove the obvious reflections and rotations, which cuts the number of tests to something closer to 60,480:

if (lxx==0) { // nothing played yet..
  if (ix>2) if (ix != 5) continue;}
else if (board==2) { // X in position 1 only
  if (ix==4) continue;
  if (ix==7) continue;
  if (ix==8) continue;}
else if (board==4) { // X in position 2
  if (ix==3) continue;
  if (ix==6) continue;
  if (ix==9) continue;}
else if (board==32) if (ix>2) continue; // X in 5
That's still too many, so I modified Xwon() to ignore zero plays so I could use it to detect potential wins by the opponent without actually running the recursion. I also moved the win test out of the main loop, so that there is no recursion at all if a win or loss is immediate. Detecting a cat's game (every row, column, and diagonal has at least one X and one O) was a little more difficult. I modelled it after Xwon(), but checked only for some X or O in each row or column. With a link to tell the computer to play (keep clicking the link to have the computer play itself) I got the program in TicTacRec.html (and TacTicRec.html for Windoze) working. It's hard to see what's happening, so I included a logging function. If you set LogUntil in the first line to some positive value (I chose 999) it will log that much text, then quit the analysis, displaying the logged text after the board. Or you can run it in my interpreter with Logging=1, again setting LogUntil=999. For my interpreter to work properly, you should also put your file name into the interpreter variable theLocn:
theLocn = "TicTacRec.html";
It will evaluate a partial game if you add the game state after it:
theLocn = "TicTacRec.html#125";
This also works in the browser, and a lot faster -- with less information, but you could add more trace lines. To try to learn why the computer played 2 for its second move instead of the better corner, I manually added "#5" to the browser URL and set the LogUntil=99999 (999 stopped early, with a different answer). I left it as an exercise for you to discover why. The full trace of the first play on a blank board produces a vast amount of output (nearly 7000 lines, one per test, well over a hundred thousand characters), but you might find it instructive.

In play mode (LogUntil=0) you can play against the computer, or have the computer play against itself. You can even step in and make one play, then let the computer take it from there.

Total Pruning

Expanding the CanWin(Gstate) function somewhat, we can use it as a scoring tool to prune the game tree much earlier. The play may not be as good, but eliminating the recursion speeds up the analysis greatly. I added a second parameter to identify which square we are scoring, then increased the score when this play added a second X (or O) to the row or column being scored. This is not necessarily the best strategy for winning Tic-Tac-Toe, but it's not bad. A reasonably good strategy (but not necessarily the best) is called a heuristic from the Greek word meaning "find" (it finds something, like a good score).

Again, I will invite you to look at the new version of the program in TicTacHeu.html (and TacTicHeu.html). Is it better or worse than the recursive version? Can you think of a way to get the best of both methods?

Next: Computer Animation

Tom Pittman
2010 December 23