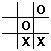
<<Previous | ToC
| Next >>
ToC This Page
Game Strategy
Display
Arrays
Top-Down Design
O Heuristic
We have built a couple simple games without a lot of hard thinking
about what the the game actually does. In Real programs, the algorithm,
the logic of the game play, or how you get your rocket to land on Mars
(and not go the other way), that's the hard part of programming. So now
we'll look at a much more complicated program. The first thing to do when
writing any program is think about what it needs to do. The professional
educators in this business call this "Problem Solving," but I think it's
more a matter of "thinking like a computer" while analyzing the problem.
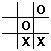
You are playing "O", so where do you play? It's a no brainer, you play bottom left, because then you win. After the mechanics of the play, getting the user's choice, updating the board, when it's the computer's turn to play,
A. You want to look for three in a line, or more precisely, you want to look for an empty square that is in the same row, column, or diagonal with two other O's for a win.In English, what do you tell the computer how to decide where to play? The computer is a step-by-step machine. What is your first step? Are you looking for an empty square? Which of our five principles would you use to find an empty square?
OK, you found an empty square, what next? Suppose you found Square 1, the top left corner. how many different directions do you need to look before you know whether you won or not? How do you decide which of those directions to try first?
OK, let's say your first choice is the top row. If O plays the top row, is that a win? How do you know?
Write down (in English) on a piece of paper, or else open a text editor,
what you just now decided to tell the computer.
Now let's say one of those O's isn't there. Where do you play? Same place, because the two X's will be three in a row if you don't. So if A doesn't tell you where to play, then
B. You want to look for an empty square that is in the same row, column, or diagonal with two X's for a block.Again in English, what do you tell the computer how to decide where to play if it sees those two X's and one O? Write it down.
Now write the same thing(s) in Java. Do you have any iteration? Do you
know how to spell iteration in Java? How do you tell it where to start?
How do you tell it when to stop?
Same board, take out all but the two corner plays, so this is what you see:
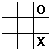
Where do you play? Obviously not in the empty square between them, that
would never combine with the existing O to become part of a win, so it's
a wasted move -- or worse, it gives the other player one more useful turn
to win by. The upper left corner builds on the row that has the O, and
it also starts the open left column, so there are several strategies we
might look at, and give them different weights depending on how aggressive
or defensive you want to be. Think about it while we focus on the mechanics
of display.
There are three parts to working with arrays: first you tell the compiler the name of the array and the data type of its elements. In Java that looks like this:
int[] TTTplays;where the type of the elements is "int" and the "[]" tells the compiler that this is an array named "TTTplays". Then, before you can do anything else with this array, you must allocate memory space for it at least once:
TTTplays = new int[10]; // or else TTTplays = new int[lxx]; // (lxx previously defined, >0)It is often convenient to do both steps in the same line:
int[] TTTplays = new int[10];If you subsequently decide you need more or fewer elements (or for any reason at all) you can allocate another array. when you assign the array variable to the new allocation, the previous contents are lost, and eventually are "garbage collected" (made available for re-use).
Arrays in Java are Objects, with all the rights and priviledges thereto, which means you can have two variables pointing to the same object, so long as they are the same (or compatible) type. If you tell the computer
int[] theSame = TTTplays;you get a second reference to the same array, so if you change the elements of TTTplays, you can fetch values out of theSame, and they will be the new values. Which brings me to the third part of working with arrays, which is putting values into the individual elements, or getting those values back out. You use an index -- sometimes called a subscript from the idea that arrays represent the mathematical concept of an indexed variable, which is written (in mathematics) as a capital letter with a tiny italic index variable hanging slightly below the line, like this:
Xi-- anyway, that would be written in Java as "X[i]" and (in our case) a reference to the value of the third element in the TTTboard array would be TTTplays[4]. Like C, all Java arrays start with index 0, so if you want the squares in your TicTacToe play board to be numbered from 1 to 9, you need to allocate an array with ten elements in it and ignore the first (TTTplays[0]) element. You can use this reference on either side of the assignment operator, that is, you can put values in, and you can look at the current value. In reality, an array is a handy way to refer to a whole bunch of similar data with a single uniform reference, differing only by the index value, which might be the control variable in a for-loop.
In our case, we could declare and allocate our board array, and then preset it to (for example) the number of its position:
int[] TTTplays = new int[10];Notice that we did not give a value to TTTplays[0], which is left undefined. It may be safe in this case, but it's probably a bad policy in general. We could alternatively make an array of the individual widgets -- any type, remember? -- on the game board:
for (int nx=1;nx<10;nx++) TTTplays[nx] = nx;
GameWgt[] TTTboard = new GameWgt[10];but then we'd need to go to all the trouble of defining the properties of each widget, which GameMaker does so much more easily for us. It would be easier (and less prone to errors) to create the nine board widgets in GameMaker, but give them carefully sequenced names "sq1" to "sq9" then let the game engine get their references for us:
for (int nx=1;nx<10;nx++) TTTboard[nx] = new GameWgt();
for (int nx=1;nx<10;nx++)You could also initialize these to their square number, but again (for only nine quares) that is easier to do in GameMaker.
TTTboard[nx] = myGame.FindListWgt("{sq" + nx + "}");
Now, for instance, you might play the X moves into this array using the formula I gave above:
int here = (vert>>6)*3+(horz>>6)+1;Then later on, after you have decided where to play O, perhaps in variavle chose, you would have the computer play O like this:
if (TTTplays[here] !=0) return false; // that square is taken
TTTplays[here] = 1; // play X there
TTTboard[here].PutTextLn("X");
if (TTTplays[chose] !=0) return false; // that square is taken
TTTplays[chose] = -2; // play O there
TTTboard[chose].PutTextLn("O");
There are two advantages to playing a -2 for the O moves.
First, by being negative (to X's positive), you can do a simple sign test
to know who played this square. Then, if you want to add up all the plays
in a particular row, column, or diagonal, three X's adds up to +3, three
O's adds up to -6, two of each adds up to +2 or -4, and one each adds up
to -1. One simple sum tells you exactly how many of each player there are
in any single row/column/diagonal. If you wanted to do that. You can get
the same effect with both numbers positive, but it's harder to find two
values that give you that property.
public static void main() {
/// some variables probably go here, dunno what
while (true) { // decide later, after drawing the board, if it's over
/// 1. Display the board..
/// 2. Is game over?
/// 3. Accept X play
/// 4. Calculate O play
} // end of outer game loop
/// congratulate winner
} // end of main program
I use three-slant comments to mark parts of the program that need
more work, so they are easy to see. Anyway, this is called "top-down design"
which was popular some years ago, but not so much lately. You still need
to do it, but maybe they have a different name for it. Whatever.
Anyway, if you try to run this program as-is, it will hang (get stuck in an infinite loop) because there is no exit from the while loop. This will happen to you a lot, get used to it. But mostly we try -- not always with success -- to prevent it. First, how to get out... In the main BlueJ window (with the two yellow rectangles), near the lower left corner, there is a horizontal barber pole which is usually black and gray stripes. When your program is running, it will be rotating red and gray stripes, which you can right-click to pop up a single-item menu to stop everything, like this:

The newer version of BlueJ has a little curvy arrow in the lower right corner that you can click to do the same thing, but the best way to prevent our budding TTT program from hanging is to provide a default termination for its outside loop, like with a for-loop. There are only nine squares, so the most number of times a play could be made is nine -- actually four and a half, because we make two plays each time around -- so I'm going to replace that open while loop with this:
for (int max=0;max<9;max++) { // default termination if game does not end normal
Even better, for a turns-based interaction with the computer, we
can make the whole program event-driven, which means the computer does
nothing at all (for us) until an event happens. The GameEngine is event-driven,
and if we
If we do the rest of the program correctly, the for-loop will always
exit early when X or O wins. This is a safety net, because mistakes happen.
There are nine squares in a TTT board, and the usual numbering is like a telephone keypad, so:
1 | 2 | 3
---+---+---
4 | 5 | 6
---+---+---
7 | 8 | 9
The first time I put this game out for students to program, I tried
to use bit arrays in a single int, which was impossibly hard to explain.
People just copied the code, but had little or no understanding of what
they were doing. That's gone now. No code for you to copy, you need to
think about how the game needs to be played, and then write your own code
to do that. If you get stuck, that's what we are here for, ask for help.
We won't tell you what code to write, but we will help you to understand
the problem so you can figure it out.
We don't need that outer loop at all. Each time the user clicks on the game board, that is their play, we get a ClickEvt method call with the coordinates of where they clicked. We just need to put an X there, then figure out where O should play. Then do it and get out. Maybe have another text widget that is hidden at the start, then when somebody wins, put up a congratulatory message. Does this make sense to you? Rewrite out high-level version of the program, but this time as a single ClickEvt method call.
How do you display the game board? You don't. GameEngine does that.
How do you figure out where to put the X? You don't. Well, not exactly. GameEngine gives you the coordinates of where the user clicked, and you divide that by the square size to get a row and column number, which is easily converted to a square number, then you put the user's X there.
Did X win? Check every row/column/diagonal and see. Remember, we discussed something like that at the front of this page. Now you get to do it.
Where should the computer play O? Go back and look at A (O wins) and B (X is blocked) above, can you do those two? If it's not one of them, can you think of any reason to play any other square? Can you describe why in plain English? Write it down. Then can you think how to say in Java what you already said in English? Is there an iteration? You know how to say that in Java, right? Is there a decision to be made, perhaps how many X's and O's there are in a given line, you know how to do conditionals in Java, right? Input? You already did that, when the user clicked. Output? that happend after you decide. What's left, variables and expression evaluation? You do that when you look in the TTTplays array to see how many X's and O's are there, right?
Think positive, "I can do this." Does O win when there are no other O's in this line? No? I didn't think so. Does O win when there is one other O in this line? How about when there are two? How can you tell the difference? You are smarter than the computer, you get to tell the computer the answer to that question.
What happens when you addup the current plays in row one?
sum = TTTplays[1]+TTTplays[2]+TTTplays[3];What does that tell you about how many O's there are in that row? Is playing in that row a good idea or a bad idea? How do you know? Think about it.
What I did is go through all the unplayed squares and assign a score (create another variable, re-initialized to zero each time before starting the analysis) based on how good a play in that square is likely to be. Obviously, if it's a winning play for O, that's the best possible play. I picked 99 as the high score. On a bigger board (a different game) there might be other ways to get a score of 99, so we would need to use a bigger "high score" number. If a candidate position is not a win for O but it blocks a win for X, that's still a very high score, just not as good as O winning. I figured that adding 22 to the current score is about right. When you do heuristics like this, sometimes you have to try several values before you find one that works. Otherwise (if not a win or block) we count the number of rows and columns through this square with one or no plays in that row yet; another O there is aggressively scored 4 points, a single X there is scored two points, and empty is scored one point. If there is already both X and O in that direction, it's playable, but worthless.
I used a for-loop to run through the board and test each square. Here is the stubbed-out version of the heuristic:
int doing, best = -1, chose = 0, score, sum;
/// 4. Calculate O play
for (doing=1;doing<=9;doing++) { // try all available squares
if (TTTplays[doing] !=0) continue; // already played, go to next square
score = 0;
/// for each row/column/diagonal doing is in, add up the sum..
/// if doing wins, score = 99
/// if doing blocks X win, score = score+22
/// if this line is empty, score++
/// if this line has one X, score = score+2
/// if this line has one O, score = score+4
/// otherwise (assume one each) no change to score
/// if score>best, remember chose = doing, best = score
} // end of heuristic for-loop
/// play chose
Let's solidify this logic in our minds before we run off in all
directions at once. How do we know if this play (whatever doing
is) would win? That would be if after you played it, there would be a win
for O. We don't actually play it yet, we just want to think about what
would happen if we did. Suppose doing=1; (the first square we
look at). How would that become a win for O? Perhaps O is already in squares
2 and three, or maybe also in 4 and 7, or else also in 5 and 9. Playing
1 in any of those three combinations is a win for O. Programmatically,
that would be (for the top row)
if (board[2]>0) if (board[3]>0) score = 99;So if you write a test for every possible row, column, and diagonal, combining the already played board with doing to see if it fills that
if (doing<4) { // in the top row..To know if the candidate play is in a particular column, we can use the remainder (modulus) operator '%' because the remainder of doing/3 will be 1 in the first column, 2 in the middle column, and zero in the right column. Convince yourself this is true.
sum = board[1]+board[2]+board[3];
if (sum == -4) score = 99;
} // end of top row test
else ...
if (doing%3 == 1) { // in the left column..You can use doing%4==1 for the down diagonal (I'll let you write it) but the up diagonal doesn't come out right that way, so the best you can do is logical-OR of three individual tests:
sum = board[1]+board[4]+board[7];
...
else ...
if ((doing==3)||(doing==5)||(doing==7)) { // in the up diagonal..
sum = board[3]+board[5]+board[7];
Can you do the rest? You need to think like a computer, so that
you understand exactly what the computer will do with this code. Then you
will know what to do for the other five lines. Try it. Program it up and
step through in the debugger. Did it do what you thought it would? Do you
now understand what it did do? This is important, you cannot tell the computer
what to do and expect it to do what you wnat if you don't know what it
will do with what you did tell it.
Then you want to know if playing there blocks X. If X played in the middle (square 5) and then in the bottom right corner, then O must block by playing the upper left corner, position 1. You know that, right? So basically you are going to run the same eight tests, but for equality to +2 (two Xs in that line) instead of -4, like this:
// in each row/column/diagonal..
if (sum == 2) score = score+22;
Maybe the row/column/diagonal is empty. If there are no Xs and no
Os there, what would the sum of those three
cells be? Zero. You can also get zero from adding two Xs plus one O,
but we already disallowed that (the candidate cannot test if the space
is already filled). Here's the test line going into each sum:
// in each row/column/diagonal..
if (sum == 0) score++;
Then if a given row/column/diagonal is not empty (==0) and it's
not a win or block or worthless (which you already checked) then it must
have exactly one mark, either X (+1) or O (-2). So you compare each of
the eight sums two more times to add +4 or +2 to the score. Can you do
that?
Finally, if there is one-each X and O in the same row -- does this begin to sound familiar? Instead of the sum being -4 (to test for a win) or +2 (to test for a block), you now add a single X (+1) and O(-2) for a sum -1 (to test for a worthless play), eight tests. You can also see why I chose -2 for playing O: there's no way to add up any combination of these two numbers to get -1, except one each. But these don't add to the score, so we can ignore them.
How much of this do you think you can write code for? Try it.
Next Up: Some Game Ideas in Java
<<Previous | ToC | Next >>
Revised: 2021 May 11x