In 2019, with the prospect of entering their car in the international F1/10th autonomous car race that fall, I proposed a more disciplined and far faster algorithm for identifying track boundary walls and possibly also visual landmarks, using Finite State Machines (FSMs). At the time I proposed generating Java source code to implement FSMs for recognizing boundary walls, but Elliot Roberts, who had signed up to do the implementation, suggested instead a table-driven approach which is insignificantly slower and substantially easier to understand and to parameterize after seeing the actual requirements prior to the race ("Pre-Race" day).
I did not at the time explain clearly how to merge individual FSMs (one for each type of boundary wall and landmark) into a single unified FSM for the whole image (one column at a time), but Elliot did a credible job of inventing a process that seemed to work. When he became unavailable to carry the development to completion, I tried to explain the merging algorithm to his successor and discovered my memory of it (as described in my 1992 textbook) was inadequate.
The purpose of this document is to explain the whole mechanism so that
a student with no prior experience or understanding of FSMs
can successfully implement it.
FSMs Defined
Implementation
Non-Deterministic FSMs (4 FSM Example) (Building It)
Another Idea
Back to TechTopics Part 11b (Tasks)
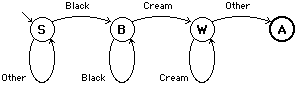
A Finite State Machine is defined as a finite number of states, one of which is designated to be a start state, and some subset of which are designated final states, and a finite alphabet (usually the characters of the input program in a scanner), in our case the colors of the image pixels being processed, posterized down to a small number, the sequence of which constitute sentences or valid input strings in the language recognized by the FSM, and a set of transition rules for advancing from one state to the next based on a single input symbol in the alphabet, as specified for each rule. Here is a diagramatic representation of a sample FSM for recognizing a room wall:

The Start state ("S") is conventionally identified by an arrow pointing to it out of nowhere, the Halting state ("A") by the extra heavy circle, and the transitions by arrows marked each with the input symbol associated with that transition, in this case the color of the pixel recognized. These colors would normally be posterized, so that any dark color is seen as "Black" and any cream-like color would be posterized as (for example, but not shown here) yellow.
The state machine advances from the start state (presumably the floor) where it stays (loops) as the state machine walks up the image from the bottom, until it reaches the baseboard of the wall to be recognized. This pixel is black (not a floor color) so the state advances to state B which remembers having see at least one black pixel. Additional black pixels continue to be recognized (transitioning to the same state) until a cream/yellow pixel is seen, so it transitions to state W, which remembers (in the state) that it now has seen both the black baseboard and at least one pixel of the cream wall paint. If any other color is see, besides black or cream while in state B, the state machine has no transition for that color, so it fails and this wall is not recognized. In state W additional wall pixels are accepted as part of the wall being recognized, but when the walk up the image reaches the top of the wall and see another color, it advances to state A and accepts that column of the image as a cream wall.
This is actually inadequate for recognizing real walls, because a single pixel of black (perhaps a wire on the floor) followed by a single pixel of cream or yellow would be accepted. We solve this by counting the number of black pixels -- counting in a FSM is done by adding states -- as in this fragment, which recognizes four black pixels in a row:

Notice that we have not defined any transition out of state B other than black, so if this FSM sees fewer than four black pixels in a row, it simply fails. Each state in the FSM remembers how many black pixels it has seen, but state E can accept any number of additional black pixels before it sees the cream wall. The result is that this FSM requires a minimum 4-pixel baseboard. You can similarly add states of cream/yellow so that the wall must be a minimum number of pixels of painted wall to be recognized.
You can also add state transitions to accommodate noise in the pixel
image -- for example some other color than black seen in state B
might return to the start state on the assumption that it's a noise pixel
to be safely ignored.
You will need several integer arrays whose length is the width of the image:
State: The current state in this column, initially =1The wall type and height are needed for determining where that part of the wall is, relative to the camera. The polar coordinate of that point in the wall can be determined from the pixel position (which can be calibrated to an angle from the heading of the camera, for a given focal length), and the distance from the camera (which is calculated from a calibrated standard height and distance at that horizontal pixel position, divided by the known measured height of that wall type). This constructed vector of wall positions can then be used for creating a cartesian map of the track on pre-race day, and then during the race for correcting drift in the perceived position of the car relative to that map.
Type: The recognized wall type in this column (initially 0 = failed to recognize)
Botm: The pixel row of the bottom of the recognized wall
Tall: The pixel height of the recognized wall
Assuming you have already converted the camera native format to RGB, and assuming the current state for this column is non-zero, the first thing you do is posterize this pixel to a small number of colors, perhaps 8 levels of gray and six simple primary and secondary hues, plus a fake "color" representing the top of the image, which fits into four bits. The state number fetched from the State array is already shifted left 4 places, so you just add the posterized color to it and use the sum to index into the transition table. This gives you a new state number (already shifted left 4 places) and 15 non-zero action codes used to tell the FSM that this is a halting state and to capture the row position and wall type. One of these 15 action codes captures the bottom row of a wall (without halting), and the others can be halting states, where the action code is the wall type. Normally the action code is zero, so you save the new state and advance to the next column. The action codes take extra time, but they only happen twice per column. The basic FSM is only four lines of code and very fast (about 10 nanoseconds per pixel in a 2GHz CPU). The posterizing is probably an order of magnitude slower, so it makes sense to omit it when the FSM is finished with this column.
When you finish the horizontal sweep, the resulting type and height
arrays are ready to be used by the client processes. You have at most 14
wall types (for a 4-bit action code), but the actual race tracks so far
(see the videos) have been limited
to three or four wall types, and too many types is an extra burden on the
hosts creating the track and therefore extremely unlikely.
The FSM engine would run only a single FSM, composited from multiple FSMs, each recognizing a single wall type. Initially the composite FSM would be non-deterministic (NDFSM), that is, it would try all possible wall types (in their respective FSMs) simultaneously and in parallel, which is impractical in software, but as outlined in my book (Pittman & Peters, The Art of Compiler Design, PrenticeHall 1992, pp.64-71), the NDFSM can be converted algorithmically to a deterministic FSM. We now look at how to do that.
You will need a software tool to do this, beginning with an input specification,
where the operator selects each of the pre-written FSMs
to use, and chooses posterized colors to plug into any parametric colors
in those FSMs. The tool will then copy those
FSM
specifications into a large array of transitions, by assigning new state
numbers for every copied state except the start state. This may result
in multiple transitions out of the start state for a single color (typically
black, which could represent a baseboard on an ordinary room wall, or the
shadow under the tube wall); if all the resulting transitions are unique,
then you are done. Otherwise, those multiple destination states represent
non-determinism, and your tool will construct a new deterministic
FSM
by the following algorithm. Suppose you are merging three wall types (a
tube wall FSM like my BetterTubeWallFSM
example code, and a room wall with a baseboard as above, plus a plain panel
such as used in Montreal, both exemplified in my SomeFSMs
example code) with a floor FSM appropriate
to the carpet pattern in the PSU conference room where we held our sessions
this summer (also in my SomeFSMs example code).
Here are (simplified versions of) the four FSMs
with the new state numbers already assigned, and the posterized color pallette
reduced to (0=black, 1=gray, 2=white, 3=yellow, 4=red, 5=panel, 6=other,
7=image top), and action #9 saves the row# as the bottom:
| Floor | Tube | Wall | Room | Wall | Panel | ||
| St.Co | nSt | St.Co | nSt+Ac | St.Co | nSt+Ac | St.Co | nSt+Ac |
| 1.0 | 2 | 1.0 | 5+0 | 1.0 | 20+0 | 1.0 | 30+0 |
| 1.1 | 1 | 5.0 | 6+0 | 20.0 | 21+0 | 1.5 | 33+9 |
| 1.4 | 1 | 5.1 | 1+0 | 21.0 | 22+0 | 30.0 | 31+0 |
| 2.0 | 3 | 5.4 | 1** | 22.0 | 23+0 | 30.5 | 33+9 |
| 2.1 | 1 | 6.0 | 7+0 | 23.0 | 24+9 | 31.0 | 32+0 |
| 2.4 | 1 | 6.1 | 1+0 | 24.0 | 25+0 | 31.5 | 33+9 |
| 3.0 | 4 | 6.4 | 1+0 | 25.0 | 26+0 | 32.0 | 1+0 |
| 3.1 | 1 | 7.0 | 8+9 | 26.0 | 27+0 | 32.5 | 33+9 |
| 3.4 | 1 | 7.1 | 1+0 | 27.0 | 27+0 | 33.0 | 0 |
| 4.0 | 0 | 7.4 | 1+0 | 27.3 | 28+0 | 33.5 | 34+0 |
| 4.1 | 1 | 8.0 | 8+0 | 28.0 | 0 | 34.5 | 35+0 |
| 4.4 | 1 | 8.1 | 9+0 | 28.3 | 29+0 | 35.5 | 36+0 |
| 9.0 | 8+0 | 29.0 | 0+2 | 36.0 | 0+3 | ||
| 9.1 | 10+0 | 29.1 | 0+2 | 36.1 | 0+3 | ||
| 10.0 | 0 | 29.2 | 0+2 | 36.2 | 0+3 | ||
| 10.1 | 11+0 | 29.3 | 29+0 | 36.3 | 0+3 | ||
| 11.0 | 0 | 29.4 | 0+2 | 36.4 | 0+3 | ||
| 11.1 | 12+0 | 29.5 | 0+2 | 36.5 | 36+0 | ||
| 12.0 | 14+0 | 29.6 | 0+2 | 36.6 | 0+3 | ||
| 12.1 | 13+0 | 29.7 | 0+2 | 36.7 | 0+3 | ||
| 13.0 | 14+0 | ||||||
| 13.1 | 13+0 | ||||||
| 14.0 | 15+0 | ||||||
| 14.1 | 13+0 | ||||||
| 15.0 | 15+0 | ||||||
| 15.1 | 16+0 | ||||||
| 16.0 | 15+0 | ||||||
| 16.1 | 17+0 | ||||||
| 17.0 | 0 | ||||||
| 17.1 | 18+0 | ||||||
| 18.0 | 0 | ||||||
| 18.1 | 19+0 | ||||||
| 19.0 | 0+1 | ||||||
| 19.1 | 19+0 | ||||||
| 19.2 | 0+1 | ||||||
| 19.3 | 0+1 | ||||||
| 19.4 | 0+1 | ||||||
| 19.5 | 0+1 | ||||||
| 19.6 | 0+1 | ||||||
| 19.7 | 0+1 | ||||||
A brief explanation of some of these FSMs is in order. The floor is observed to have speckles of black and several shades of gray (here all posterized to color #1), with a hint of reddishness that occasionally gets posterized to red #4. This FSM accepts any number of red or gray pixels without counting them because no wall starts in those colors. In particular, where the floor is out of focus or smudged by distance, all the speckles blur into a uniform gray, so it makes no sense to count those pixels. Black pixels were observed to be limited to runs of six or fewer (here simplified to three), so that any run of more than that maximum run causes the floor FSM to fail, but presumably any wall FSM starting in that many black pixels can continue running.
I simplified the tube-wall FSM to require a minimum of four initial (floor-level) black pixels (fewer than the minimum reverts to the floor state #1) followed by a minimum of five gray pixels followed by at least two black pixels (the shadow between the two tubes) followed by a minimum of four more gray pixels before it accepts (action #1) on any color other than gray.
The simplified room-wall FSM requires a minimum of eight black pixels as a baseboard before looking for at least two (yellow) pixels. It may accept where the wall hits the ceiling (if the ceiling is a significantly different color) or else at the top of the image where we have a bogus top-of-image color to trip the recognizer (that was Elliot's idea, and a good one), but the height of the wall is useless. A more useful output could be generated if you declare the wall top to be at the transition from baseboard to plaster (or a couple of confirmatory pixels thereafter), so you can actually measure the distance to the wall. I leave that to the student as an exercise.
The plain panels used as track wall in Montreal might have a thin (optional) shadow at the bottom, which is assumed to be no more than three pixels, after which it is assumed we are still looking at the floor. The bottom of the panel comes with the first pixel seen as panel-colored, and at least four of them must be seen (otherwise the FSM fails), thereafter any color other than panel color is the top of the panel and it accepts.
Now we have four different colors that can be seen (with their own state
transitions) out of the start state, but black (color #0) nondeterministically
can transition to any of the states #2, 5, 20, or 30. In other words, when
the resulting deterministic FSM sees black
out of the start state, it could be either another floor pixel, or the
shadow under a tube wall or a plain panel, or else the baseboard under
the room wall, and we don't know which yet.
Starting with a blank FSM, add a start
state -- call it S, to minimize confusion; it will later be state #1 in
the new
FSM -- then for each color that has
a transition out of the current state being considered (initially state
S) create a new state representing all of the original states you have
a transition out of that state (state #1), in this case {33} for the panel
color #5 (call it state A), and {2,5,20,30} for color #0 black (new state
B); the other two colors (#1 gray and #4 red) loop back to the start state
S. The new table with the first state filled in looks like this:
| #0 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | (colors) | ||
| (States) | S: | B | S | S | A | -- S=start | ||||
| A: | -- A={33} | |||||||||
| B: | -- B={2,5,20,30} |
Now we fill in the transitions for each new state in turn. New state
A represents only previous state #33, so only its one transition is copied
over, to new state {34}=C. New state B represents the aggregate of four
states {2,5,20,30} so we add to its line all the transitions for all those
states. If there are multiple transitions on a single color, this creates
a new aggregate state, as for example on black #0: 2->3, 5->6, 20->21,
and 30->31 so we create a new state D = {3,6,21,31}. The other transitions
are deterministic, on gray #1 and red #4 back to the start state, and on
panel color #5 to {33} which we already have as state A, so it looks like
this:
| #0 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | (colors) | ||
| (States) | S: | B | S | S | A | -- S={1} | ||||
| A: | C | -- A={33} | ||||||||
| B: | D | S | S | A | -- B={2,5,20,30} | |||||
| C: | -- C={34} | |||||||||
| D: | -- D={3,6,21,31} |
We repeat the process for each new state, until the whole table is
filled in, like this:
| #0 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | (colors) | ||
| (States) | S: | B | S | S | A+9 | -- S={1} | ||||
| A: | C | -- A={33} | ||||||||
| B: | D | S | S | A+9 | -- B={2,5,20,30} | |||||
| C: | F | -- C={34} | ||||||||
| D: | H | A+9 | -- D={3,6,21,31} | |||||||
| E: | +2 | +2 | +2 | E | +2 | +2 | +2 | +2 | -- E={29} | |
| F: | G | -- F={35} | ||||||||
| G: | +3 | +3 | +3 | +3 | +3 | G | +3 | +3 | -- G={36} | |
| H: | I | S | S | A+9 | -- H={4,7,22,32} | |||||
| I: | J+9 | S | S | -- I={8,23,1} | ||||||
| J: | K | O | -- J={8,24,2} | |||||||
| K: | L | O | -- K={8,25,3} | |||||||
| L: | M | O | -- L={8,26,4} | |||||||
| M: | M | O | AA | -- M={8,27} | ||||||
| N: | N | O | -- N={8} | |||||||
| O: | N | P | -- O={9} | |||||||
| P: | Q | -- P={10} | ||||||||
| Q: | R | -- Q={11} | ||||||||
| R: | U | T | -- R={12} | |||||||
| T: | U | T | -- T={13} | |||||||
| U: | V | T | -- U={14} | |||||||
| V: | V | W | -- V={15} | |||||||
| W: | V | X | -- W={16} | |||||||
| X: | Y | -- X={17} | ||||||||
| Y: | Z | -- Y={18} | ||||||||
| Z: | +1 | Z | +1 | +1 | +1 | +1 | +1 | +1 | -- Z={19} | |
| AA: | E | -- AA={28} |
Note that the fail transitions (blank spaces) in your NDFSM do not contribute to the generated FSM; they represent a sequence of colors that is not recognized, so the deterministic FSM must abandon that sequence, while continuing to pursue the sequences that have valid transitions on those colors.
Note also that if a collection of states in your NDFSM is not exactly the same as an existing new state, you must make another new state for it because the state remembers exactly how it got there, and if you were to combine different collections, your FSM would misbehave. For example, original state #8 is a state by itself (N) but also represented in new states I,J,K,L, and M, all of which differ in the other (original) states of their collection.
Note that I did not explain how to do state transitions where the original FSM did some action (like remembering in the Botm array the row# where it thought a wall bottom might be), because these action items are not part of the formal automata theory, but sort of laid on top to get extra horsepower out of it. As a result, you need to be very careful how you do that. In this table, each of the three wall types designates an action item +9 to remember where it thinks the wall bottom is, but the different FSMs have different opinions about where that should be. I would choose a compromise bottom that works for each wall -- the last bottom to be noticed will usually be what you get to base your wall heights on -- which might require some ad-hoc fixups to the various wall heights to get correct values. I didn't do that here, I just poked them in where they were in the original. Similarly, if you design a FSM for a single-tube wall, then it will probably "recognize" the bottom half of a double-tube wall; there is no clean fixup for that, so you may need to be satisfied with just a single-tube wall and make allowances in your code elsewhere.
Now finally you can flatten this 2-dimensional table into the 1-dimensional
table that your FSM engine reads.

You can code into your FSMs a great deal
of latitude to deal with flaws in the camera image, but you can also save
yourself a lot of trouble by using a reasonable amount of Gaussian
blur on the original image before posterizing. This especially important
with some varieties of tube-walls, because the tubing material has a lot
of wrinkles that cast extra small shadows and throw the FSM
off track. Fortunately, you can afford for your FSM
to miss up to half the pixel columns and still get reasonable wall heights
using linear interpolation and then (in the client) averaging over the
multiple samples the camera will give you as the car rolls along the track.
I built this table by hand, which is very tedious (and I probably made
some mistakes). You would not do that, but rather write a program to build
it (but if you discover errors, let me know, so I can fix them).
Part of their alternate plan involved scanning the image from the top instead of the bottom, because the room walls they were experimenting near were reasonably plain and flat, and the carpet heavily patterned. If you look at the videos for the actual F1/10th races so far, you will see that portions of the background are very busy, and any attempt to find the wall tops against that kind of background will fail far more often than it succeeds. That is why I designed my solution to scan the image bottom-up: although the carpet or terrazzo flooring is also noisy, it is a well-defined set of colors that can easily be programmed around, especially with a FSM that can look for particular sequences of colors if necessary -- hence the requirement in my solution for a separate FSM that recognizes (and passes over) the floor pattern. This is not a fatal flaw in their solution: they too could start at the bottom and subtract out the floor colors.
They seemed to think that remembering where the wall top and bottom was in the previous column of pixels could save time in searching for the top and bottom in the next column over, and this is perhaps mostly true. The FSM engine is very fast (about 10ns per pixel, far faster than their search mechanism, and both their search heuristic and the FSM solution are at least an order of magnitude faster than the posterizing code (no matter whose is used), so the actual search time is dwarfed by the posterizing. They did their posterizing in a separate pass through the data, which means that not only are they accessing pixel data arrays three times more often -- the for-loop overhead in most compilers is only three machine instructions, which is completely insignificant compared to the actual processing being done, but array access in Java involves a pointer null-check and dereference and then the array index calculation and bounds check, at least an order of magnitude more expensive than the for-loop overhead -- but also they cannot avail themselves of the optimization I mentioned above, where the posterizing can be completely eliminated for those parts of the image where the wall information is already known, which can save up to 30% in the FSM implementation or as much as 80% in their own code, if they implement it intelligently in a single pass through the pixels.
As explained to me, their scheme involved placing the camera on pre-race day in front of each wall type, then optimizing the posterizing process for that wall type -- I think they meant to maximize the color differences, but the explanation did not make that clear -- after which they would search the image for those colors. It was not at all clear how they would know which wall type's colors they would be looking for (when the identification of that wall type is the point of the exercise), nor how they would be distinguishing those colors from background noise behind the walls at the very edge they were looking for, when the background noise was not in the image portions they had their tool optimizing.
Finally, their proposal was said to involve some sort of optimization of the posterizing process. I don't think they'd thought it through very clearly, but if you don't do the posterizing based on creating saturated colors, then each pixel being posterized must necessarily involve comparing upper and lower bounds on each of the three (RGB) component colors for each of the poster colors they have chosen, perhaps as many as forty comparison-tests (versus a dozen or so in my posterization code example in TrakSim). A better implementation would use a humongous lookup table, which would be reasonably fast (and memory is cheap), but still suffer from the other problems.
Even if they do not solve these problems that the FSM is already optimized for, it is unlikely that their proposal will run so slow as to scuttle the race-worthiness of the car, because at pre-race time the car can go as slow as necessary for memorizing the track, and on race day, the image processing can perform adequately if they discard three out of every four frames to make more time for processing the rest. The worse problem is that their proposal is so complicated and error prone and ill conceived that the implementation time and especially the debugging time will most likely delay the readiness of the car to beyond the time for the race. The FSM is at least conceptually simple, so that the code to implement it can be written in a day or two and debugged in a week or so -- at least by somebody who believes it will work and wants to work on it. But my opinions today are based on working code and a lifetime of experience designing and building high-performance software; that is obviously no competition for high school students who are already known to suppose themselves immortal, and (in this context) probably also omniscient.
Tom Pittman
Rev. 2019 August 15